Corrigé du baccalauréat Terminale ES Polynésie 21 juin - Apmep

?Corrigé dubaccalauréat Terminale ES Polynésie 21 juin 2019?
Exercice14points
Commun à tous les candidats
1.Soitfla fonction définie et dérivable sur ]0 ;+∞[ d"expressionf(x)=-1,5x2+x2ln(x).
La fonction dérivée defest donnée pour toutxde ]0 ;+∞[ par :
a.f?(x)=-x+1b.f?(x)=2xln(x)-2x
c.f?(x)=-3x+2d.f?(x)=-xln(x)-0,5x
f(x)=-1,5x2+x2ln(x) donc
f?(x)=-1,5×2x+?
2x×ln(x)+x2×1x?
=-3x+2xln(x)+x=2xln(x)-2x
2.Entre 2006 et 2018, dans un restaurant universitaire, le prix d"un repas est passé de 2 euros à
3,50 euros en augmentant chaque année dex%. Parmi ces valeurs, la valeur la plus proche de
xest :
a.6,25b.4,77
c.14,58d.0,85
Il y a 12 ans entre 2006 et 2018. Le nombrexest tel que 2×(1+x)12=3,5; ce qui veut
dire quex=?3,5
2?
1
12-1≈0,0477 qui correspond à 4,77%.
3.Un adolescent joue à un jeu dont les parties successives sontindépendantes.
À chaque partie, il a une chance sur 25 de sortir vainqueur.
Après 13 parties, à 10
-3près, la probabilité qu"il ait gagné au moins une fois est :
a.0,588b.0,412
c.0,025d.0,975
L"événement "il a gagné au moins une fois» est l"événement contraire de "il n"a ja-
mais gagné» qui est de probabilité?24
25?
13
.
La probabilité cherchée est donc 1-?24
25?
13
≈0,412.
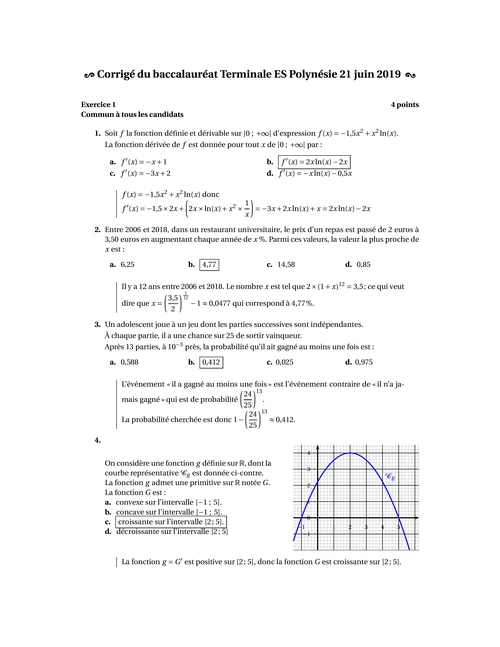
4.
Onconsidèreune fonctiongdéfinie surR,dontla
courbe représentativeCgest donnée ci-contre.
La fonctiongadmet une primitive surRnotéeG.
La fonctionGest :
a.convexe sur l"intervalle [-1 ; 5].
b.concave sur l"intervalle [-1 ; 5].
c.croissante sur l"intervalle [2; 5].
d.décroissante sur l"intervalle [2; 5]1 2 3 4 5-10
-11
234
Cg
La fonctiong=G?est positive sur [2; 5], donc la fonctionGest croissante sur [2; 5].
Corrigédu Baccalauréat ES/LA. P. M. E. P.
Exercice25points
Commun à tous les candidats
Une entreprise vend des téléviseurs.
PartieA
Une étude a montré que ces téléviseurs peuvent rencontrer deux types de défauts : un défaut sur la
dalle, un défaut sur le condensateur.
L"étude indique que :
•3% des téléviseurs présentent un défaut sur la dalle et parmiceux-ci 2% ont aussi un défaut
sur le condensateur.
•5% des téléviseurs ont un défaut sur le condensateur.
On choisit au hasard un téléviseur et on considère les évènements suivants :
•D:"le téléviseur a un défaut sur la dalle»;
•C:"le téléviseur a un défaut sur le condensateur».
1. a.3% des téléviseurs présentent un défaut sur la dalle, doncp(D)=0,03, et parmi ceux-ci
2% ont aussi un défaut sur le condensateur, doncpD(C)=0,02.
5% des téléviseurs ont un défaut sur le condensateur, doncp(C)=0,05.
b.On complète dans l"arbre ci-dessous les pointillés par les probabilités associées :
D
0,03
C0,02
C1-0,02=0,98
D
1-0,03=0,97C
C
c.p(D∩C)=p(D)×pD(C)=0,03×0,02=0,0006
d.Le téléviseur choisi a un défaut sur le condensateur.La probabilité qu"il ait un défaut sur la dalle estpC(D)=p(D∩C)
p(C)=0,00060,05=0,012
e.La probabilité que le téléviseur choisi ait un défaut sur le condensateur mais pas de défaut
sur la dalle estp?
D∩C?
.
D"après la formule des probabilités totales,p(C)=p?
D∩C?
+p?
D∩C?
; on sait que
p(C)=0,05 donc 0,05=0,0006+p?
D∩C?
doncp?D∩C?
=0,05-0,0006=0,0494.
2.On noteTla variable aléatoire qui, à chaque téléviseur prélevé, associe le temps exprimé en
moisavantlapremièrepanne.OnadmetqueTsuitlaloinormaled"espéranceμ=84etd"écart
typeσ=6.
a.La probabilité qu"un téléviseur tombe en panne pour la première fois après 72 mois d"uti-
lisation estp(T>72)≈0,98.
b.La probabilité que la première panne arrive entre 6 années (soit 72 mois) et 8 années (soit
96 mois) d"utilisation estp(72?T?96)≈0,95.
c.Le téléviseur n"a pas eu de panne après 6 années d"utilisation.
La probabilité qu"il tombe en panne avant 8 années d"utilisation est
p
T?72(T?96)=p((T?72)∩(T?96))
p(T?72)=p(72?T?96)p(T?72)≈0,95450,9772≈0,98.
Polynésie221 juin 2019
Corrigédu Baccalauréat ES/LA. P. M. E. P.
PartieB
Afin de satisfaire davantage de clients, l"entreprise décide d"apporter des améliorations à son service
d"assistance. Après quelques mois de mise en place du nouveau service, elle affirme que 90% des
clients sont maintenant satisfaits. Un service de contrôleindépendant veut vérifier cette affirmation.
Pour cela il interroge au hasard 300 clients. Parmi eux, 265 affirment être satisfaits.
On va tester l"hypothèse "90% des clients sont satisfaits» sur un échantillon de taille 300.
n=300?30,p=0,9 doncnp=270?5 etn?1-p?=30?5 donc on peut utiliser un intervalle de
fluctuation asymptotique au seuil de 95% pour vérifier ou infirmer cette hypothèse.
I=???
p-1,96?
p?1-p?
?n;p+1,96?
p?1-p?
?n???
=?
0,9-1,96?
0,9×0,1?300; 0,9+1,96?
0,9×0,1?300?
≈
?0,866 ; 0,934?
Dans l"échantillon choisi, la fréquence de clients satisfaits estf=265
300≈0,88.
f?Idonc, au vu de cet échantillon, on ne peut pas remettre en cause l"affirmation de l"entreprise.
Exercice35points
Candidatsn"ayantpas suivi l"enseignementde spécialité
Sur un site de vente en ligne, Antoine a commandé une machine àcafé à capsules.
1.Chaque capsule achetée à l"unité coûte 0,60?.
Une offre permet d"acquérir 150 capsules au prix de 60?, ce qui fait60
150=0,40?à l"unité.
La réduction est donc de 0,20 sur 0,60 soit un tiers donc 33,33%.
2.Au 1erjanvier 2017, on comptait 60000 utilisateurs de cette machine à café.
Onestime que chaque mois, 10% despropriétairescessent del"utiliser mais oncompte 24000
nouveaux utilisateurs.
a.Soit(un)la suite modélisant le nombre d"utilisateurs de cette machine à cafénmois après
le 1
erjanvier 2017. Au 1erjanvier 2017, on comptait 60000 utilisateurs de cette machine à
café doncu0=60000.
Retirer 10%n c"est multiplier par 0,9. On passe du moisnau moisn+1 en multipliant par
0,9 puis en ajoutant 24000.
On peut donc dire que pour toutn,un+1=0,9un+24000.
b.On considère la suite(vn)définie, pour tout entier natureln, par :vn=un-240000. On
peut donc dire queun=vn+240000.
•vn+1=un+1-240000=0,9un+24000-240000=0,9(vn+240000)-216000
=0,9vn+216000-216000=0,9vn
•v0=u0-240000=60000-240000=-180000
Donc la suite (vn) est géométrique de raisonq=0,9 et de premier termev0=-180000.
3. a.On en déduit que, pour toutn, on avn=v0×qn=-180000×0,9n.
b.Pour tout entier natureln,un=vn+240000=240000-180000×0,9n.
4.Pour déterminer au boutde combien demois le nombre d"utilisateurs de cette machine àcafé
dépassera pour la première fois 230000, on résout l"inéquationun?230000 :
u
n?230000??240000-180000×0,9n?230000??240000-230000
180000?0,9n
??
5
90?0,9n??ln?590?
?ln(0,9n)??ln?590?
?nln(0,9)??ln?5
90?
ln(0,9)?n
Polynésie321 juin 2019
Corrigédu Baccalauréat ES/LA. P. M. E. P.
Orln?590?
ln(0,9)≈27,4 donc le nombre d"utilisateurs dépassera la première fois 230000 le 28emois.
5.L"entreprise qui fabrique cette machine à café prétend qu"elle touchera un certain mois plus
de 250000 utilisateurs.
u
n=240000-180000×0,9ndonc, pour toutn,un5
X←X+0,01
Y←0,5X2-7X+14+6?ln(X)
Fin Tantque
À la finde l"exécution del"algorithme, la variableXcontient la valeur 2,56, première valeur
au centième pour laquelleY>5.
3.Le coût moyen annuel de fabrication d"un pneu est minimal quand la fonctionfatteint son
minimum c"est-à-dire pourx=6; c"est donc pour la fabrication de 600 pneus que le coût
moyen annuel de fabrication d"un pneu est minimal. Ce coût est, en euro, def(6)×100≈75.
PartieB
Cette même entreprise envisage la fabrication de semoirs (gros matériel agricole).
On admet que la fonctiongdéfinie sur l"intervalle?0 ; 100?parg(x)=2x-1+e0,05xmodélise le coût
de fabrication, exprimé en centaines d"euros, dexsemoirs.
1.Sur l"intervalle?0 ; 100?, la fonctionga pour primitive la fonctionGdéfinie par
G(x)=x2-x+e0,05x
0,05=x2-x+20e0,05x.
2.La valeur moyennemde la fonctiongsur l"intervalle?0 ; 100?est :
m=1
100-0?
100
0
g(x)dx=1100?G(100)-G(0)?=1100??9900+20e5?-(20)?=9880+20e5
≈128,46
3.Le coût moyen d"un semoir est donc, en euro, 128,46×100=12846.
Polynésie621 juin 2019