algèbre matrices

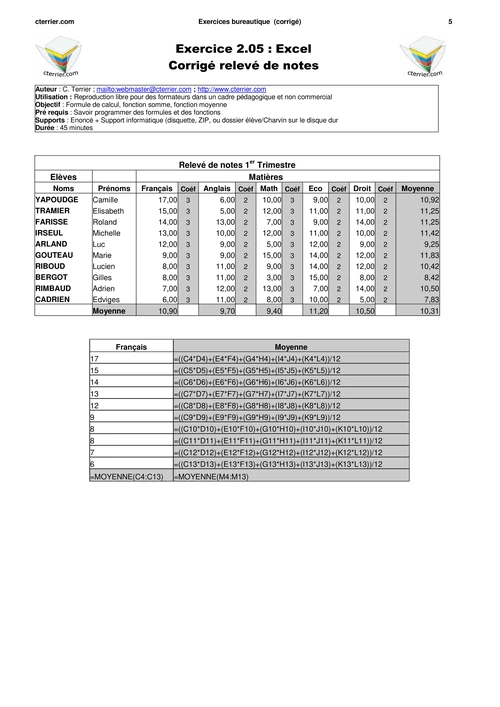EXERCICES: ALGEBRE LINEAIRE. # 1. MATIERES ... V,+ est un groupe
commutatif : - X + Y = Y + X (+ est interne, partout définie, commutative). - X + (Y +
Z) ...

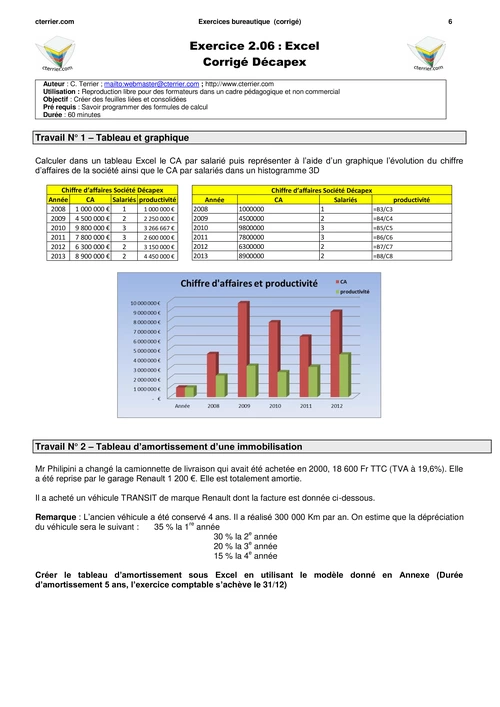Algèbre linéaire, diagonalisation. Déterminer les valeurs propres et les vecteurs
... Pour chacune des matrices A de l'exercice 1, dire si elle est : a) inversible ;.

faire connaître l'algèbre matricielle et diverses méthodes de résolution de
systèmes d'équations linéaires ;. ? faire connaître le calcul vectoriel et la
géométrie vectorielle du plan et de l'espace ;. ? développer l'acuité de la
perception spatiale ;. ? développer la capacité de faire des démonstrations ;. ?
développer les capacités ...

Solution des exercices 1. Deuxième semaine, chapitre 2 ... 357. Solution des
exercices 4. Cinquième semaine , examen 1 et chapitre 5 : Vecteurs
géométriques ...

Activité de laboratoire : Laboratoire 5 ( Maple) : Nombres complexes, p. 395.
Dixième semaine, chapitre 9 : Produits de vecteurs ...

CHAPITRE 2 : Espaces vectoriels. 2.1 Notions de groupe et de corps. 2.2
Définition d'un espace vectoriel. 2.3 Sous-espaces vectoriels. 2.4 Combinaisons
linéaires et sous-espace engendré. 2.5 Vecteurs linéairement .... à l'examen intra
, la pondération de l'examen final sera de 80 % (35 % + 45 %). À noter que des ...

Ce cours traite de deux branches des mathématiques : l'algèbre linéaire et la
géométrie vectorielle. ... matrices, déterminants et systèmes d'équations linéaires
.

Maîtriser les notions de base de l'algèbre linéaire, à savoir espaces vectoriels,
bases, applications linéaires, matrices et changement de bases. Types d'
enseignement. Présentiel. Modalités d'évaluation. Un contrôle continu (CC) et un
examen (Ex) : Note 1ère Session= (CC+2*Ex)/3 ; Note 2e Session= (CC+4*Ex)/5.

L'objectif de ce module est de donner les connaissances nécessaires concernant
la différentiabilité d'une fonction de plusieurs variables, les généralisations ...